Abstract
The Sequencer Pattern is a design pattern that addresses a common but often overlooked problem in software: how to model values that progress step-by-step within boundaries, optionally wrapped around, and are often composable to create larger structures. From timekeeping systems to currency calculations, this pattern surfaces across countless domains. The key features of a sequencer are its ability to handle bounded progression, wrap-around behavior, and composability. It centralizes the logic for incrementing or decrementing a value, checking if it has hit a boundary, and performing an action (like resetting or carrying over) when a limit is reached.
Problem
Almost everything around us, has a notion of circularity in its very nature. Across many domains, systems deal with values that move through well-defined progressions. These values don’t just increment linearly, they wrap around, cascade, or trigger side effects. Common examples include time, money, financial durations, payment cycles, calendars, simulations and many more. Consider:
- Seconds cycling from 0 to 59 and then triggering the next minute.
- Cents incremented up to 99 before rolling into the next dollar.
- Days progressing through varying month lengths before flipping the year.
These sequences typically operate within a fixed boundary, must wrap or reset on overflow, and often propagate side-effects to adjacent units when they cross thresholds.
The Hidden Nature of Progression
Software is designed to model and solve problems from the world around us, and that world is full of motion and cyclical patterns. Values move forward, time ticks on, and states cycle. For example, a payment cycle might move forward until the end of a financial year, wrap around, and then start from the beginning in the next financial year. Yet, despite how central these progressions are to our systems, we rarely give them a name or pattern. They are often implemented ad hoc: a few lines of increment logic here, a boundary check there, a silent reset somewhere else. Over time, these implementations become scattered, redundant, and fragile.
Still, the idea of bounded progression shows up everywhere. Hours on a clock, days in a month, or frames in an animation, each follows a predictable pattern of forward movement within limits. When a boundary is hit, we often reset, wrap around, or carry forward to the next layer in a hierarchy or backward in case of wanting to see the history or it’s an essential feature in case of like moving a warm in a maze game. And yet, we often model these as plain integers or switch statements, missing an opportunity to extract a reusable abstraction.
When modeled manually, this behavior leads to redundant logic, copy-pasted conditions, and brittle interactions. As sequences get composed (e.g., seconds => minutes => hours), the risk of bugs increases. Without a centralized abstraction, developers are left to hand-roll wrapping logic in domain-specific code, often inconsistent. Over time, maintaining these patterns becomes complex, error-prone, and hard to scale.
Everyday Cycles in Complex Systems
Across various domains, from the analog world to digital systems, we encounter bounded sequences. These progressions follow a set pattern of forward/backward movement within defined limits. For instance, a clock’s seconds sequencer advances from 0 to 59. Upon reaching 60, it resets to 0 and triggers the parent minutes sequencer to increment. This cascading effect continues from minutes to hours, and hours to a 24-hour cycle, forming a hierarchical system of sequencers. A time duration is another example; it’s a cumulative value with discrete, bounded boundaries, such as a video timeline that advances second by second but stops at a predefined length.
Another great example is in an accounting system where a financial year is composed of reporting periods. A weekly payment cycle acts as a child sequencer. With a 12-month year, this sequencer has a length of 52. After reaching the 52nd period, it wraps around, signaling the start of the next financial year’s cycle.
In financial software, a minor unit like cents acts as a sequencer. It advances from 0 to 99. When a value of 100 is reached, the cents sequencer resets to 0 and triggers the parent dollars sequencer to increment by one. This mechanism cleanly handles the aggregation of subunits into a higher unit.
In a digital audio workstation, a musical sequencer might advance through the 12 notes of a chromatic scale (seven main notes plus five sharps and flats). After the last note is played, it wraps back to the first, but at a higher pitch, triggering a parent sequencer that represents the octave.
All these examples share a universal structure: a value within bounds, a rule for stepping, a response to limits, and, often, a connection to a parent or child sequence. This powerful and universal structure is what the Sequencer Pattern formalizes.
Why Ad-Hoc Logic Breaks Down
Without a common abstraction, developers tend to reimplement sequencing logic from scratch for every new use case. The result is duplication of logic, inconsistent behavior, and subtle boundary bugs, like the infamous “off-by-one” errors or misfires in rollover logic.
Consider modeling a digital clock: you might manually increment seconds and, upon hitting 60, reset to zero and increment minutes. But what happens when you reuse this logic in a stopwatch, a countdown timer, or a calendar app? Suddenly, you’re copying and tweaking fragile boundary conditions, testing every edge case, and losing sight of the bigger design.
By not treating sequencing as a first-class pattern, the code becomes rigid. You can’t easily reuse a clock’s logic to model a currency system or a game loop, even though the underlying behavior, bounded progression, is identical.
Solution: The Sequencer Pattern
The Sequencer Pattern provides a generalized abstraction for modeling bounded, step-wise progressions. At its core, a Sequencer encapsulates the complete logic, including:
- State: The current value within the sequence, managed by defined minimum and maximum boundaries.
- Step Size: The number of units the sequencer moves forward or backward with each transition.
- Transitions: The logic for moving next() or previous(), which handles wrap-around behavior.
- Event Hooks: The ability to trigger side effects at boundaries, such as carrying over to another sequencer.
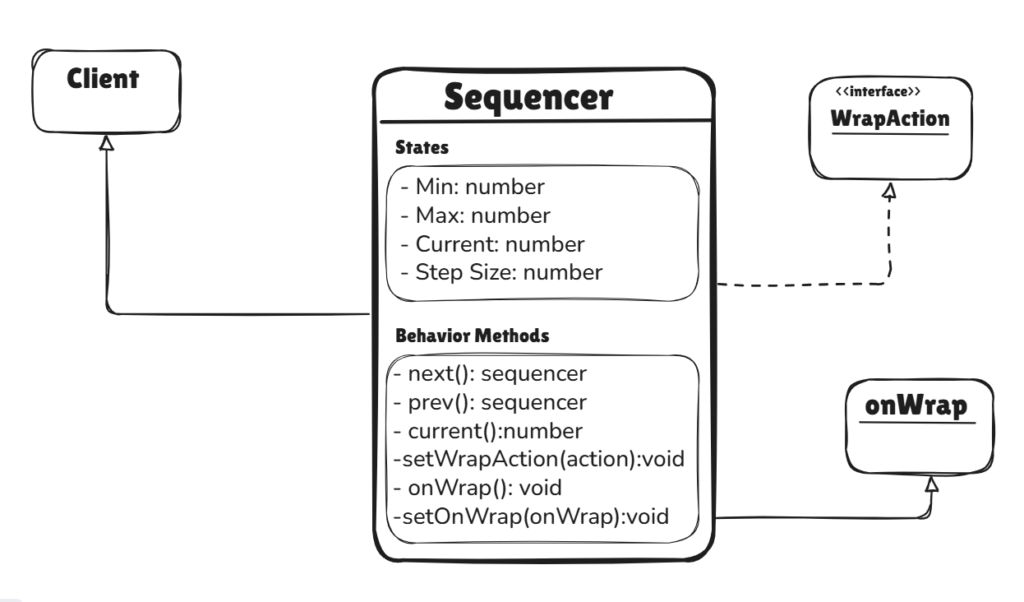
This pattern makes progression explicit and composable, allowing you to encapsulate how a value ticks forward or backward within constraints. It replaces scattered, ad-hoc logic with a reusable and predictable control structure.
Here’s a minimal example:
class Sequencer {
// State and Step Size
constructor(min, max, current = min, step = 1) {
this.min = min;
this.max = max;
this.current = current;
this.step = step;
this.onWrapCallback = null;
}
// Event Hook
onWrap(callback) {
this.onWrapCallback = callback;
}
// Transitions(forward)
next(step = this.step) {
this.current += step;
if (this.current > this.max) {
this.current = this.min;
if (this.onWrapCallback) {
this.onWrapCallback();
}
}
return this.current;
}
// Transitions(backward)
previous(step = this.step) {
this.current -= step;
if (this.current < this.min) {
this.current = this.max;
if (this.onWrapCallback) {
this.onWrapCallback();
}
}
return this.current;}}Real-World Examples
Across various domains, the Sequencer Pattern finds natural applications where discrete, bounded values interact and cascade. This powerful, universal structure formalizes a behavior we often see in both the digital and physical worlds.
Timekeeping
A clock is a quintessential example of nested sequencers. The seconds sequencer advances from 0 to 59. When it wraps back to 0, it triggers the minutes sequencer to advance. This cascading effect continues up the hierarchy to hours, days, and years. The pattern mirrors how clocks and calendars naturally function.
// Assume a Sequencer class with a customizable step and onWrap() hook
// 1. Set up the time units as individual sequencers
const second = new Sequencer(0, 59);
const minute = new Sequencer(0, 59);
const hour = new Sequencer(0, 23);
// 2. Compose the sequencers using event hooks
// When the second sequencer wraps, it triggers the minute sequencer's next() method.
second.onWrap(() => minute.next());
// When the minute sequencer wraps, it triggers the hour sequencer's next() method.
minute.onWrap(() => hour.next());
// 3. Drive the progression
// This function simulates a single tick of the clock.
function tick() {
second.next();
}
// Example usage
setInterval(tick, 1000); // Calls the tick function every secondCurrency
Financial systems use sequencers to manage different units of currency. A cents sequencer might advance from 0 to 99. When a value of 100 is reached, the cents sequencer resets to 0 and triggers the parent dollars sequencer to increment by one. This mechanism cleanly handles the aggregation of subunits into a higher unit, as shown in this example:
const cents = new Sequencer(0, 99);
const dollars = new Sequencer(0, Infinity);
// When the cents sequencer wraps, it triggers the dollars sequencer to increment.
cents.onWrap(() => dollars.next());
function addCent() {
cents.next();
}This composition is a key feature of the pattern, enabling complex systems to be built from simple, reusable components.
Calendars
Calendars are another hierarchical system of sequencers. The days sequencer advances until it hits its boundary (e.g., 30 for April). When it wraps, it triggers the months sequencer to advance. This, in turn, can trigger the years sequencer, elegantly handling the rollover logic of a calendar system.
const day = new Sequencer(1, 30);
const month = new Sequencer(1, 12);
const year = new Sequencer(2020, 2099);
function nextDay() {
if (day.next() === 1) {
if (month.next() === 1) {
year.next();
}
}
}Composition & Extensions
The true power of the Sequencer Pattern emerges when individual sequencers are composed into chains or trees. This allows you to model hierarchical progressions, like those found in a digital clock or a financial ledger, in a clean and organized way.
For instance, you can easily link sequencers so that a transition in one automatically triggers a transition in the next.
// Time Composition: Second => Minute => Hour
second.onWrap(() => minute.next());
minute.onWrap(() => hour.next());
The pattern is also flexible enough to handle more advanced cases, such as adjusting boundaries at runtime. A calendar system, for example, requires the number of days in a month to change based on the month and year. This can be handled by extending the Sequencer to use a dynamic boundary.
function getDaysInMonth(year, month) {
// Returns the number of days in a given month and year
return new Date(year, month, 0).getDate();
}
class DynamicSequencer extends Sequencer {
constructor(min, maxProvider) {
super(min, maxProvider());
this.maxProvider = maxProvider;
}
next() {
this.max = this.maxProvider();
return super.next();
}
}This adaptability enables the Sequencer Pattern to manage real-world complexity while maintaining a modular design.
How It Differs From Other Patterns
The Sequencer Pattern often resembles other well-known patterns at first glance, like iterators, counters, or even state machines, but diverges meaningfully in purpose, behavior, and intent.
Iterators vs. Sequencers
An iterator is a one-way street. It progresses through a collection or range until the end is reached, at which point it’s considered exhausted or done. Iterators don’t inherently know or care about boundaries, they’re meant to traverse, not loop.
A sequencer, by contrast, is designed to operate within boundaries and to repeat, loop, or wrap. Rather than terminating at the end of a range, it cycles back to the beginning or triggers a transition. For example, seconds rolling from 59 back to 0 is not something an iterator models well, but a sequencer handles it naturally.
Counters vs. Sequencers
A counter increments a numeric value, usually by one. It’s linear, stateless beyond the value itself, and unaware of boundaries or context. A counter might count upwards infinitely or until manually stopped.
A sequencer extends this idea with boundary awareness and richer semantics. It knows its min and max, can move forward or backward, and crucially, can delegate behavior when limits are reached. It can say, “I’ve wrapped, notify the next sequencer,” which enables compositional systems like minutes carrying into hours or cents into dollars.
State Machines vs. Sequencers
A state machine models transitions between named states (like “Loading”, “Success”, “Error”), often with clearly defined triggers or events. The logic centers on rules that govern state transitions.
While a sequencer also transitions between positions, it doesn’t care about named states, it moves numerically or logically along a progression. It’s not about symbolic states but ordered advancement, where reaching the end doesn’t mean stopping, but perhaps starting over, bouncing back, or cascading to another unit.
Enums vs. Sequencers
Enums define static, often unordered symbolic values. They represent distinct cases, like Pending, Shipped, Delivered. Enums are not designed to step, wrap, or evolve over time, they are declarative, not dynamic.
In contrast, sequencers are inherently active. They evolve, shift, and loop. They model motion across an ordered space, not identification of static labels.
Applications in Practice
The Sequencer Pattern has found practical use across various domains where managing discrete, bounded progressions is crucial.
In calendar-agnostic systems like Quantum.Tempo, the pattern powers recurrence rule parsing, fuzzy date range navigation, and the traversal of multi-calendar systems. Each calendar field, such as a month, day, or week, becomes a sequencer that can be composed and coordinated to accurately model time and events.
For distributed systems, ID generators like Snowflake often use sequencers to produce high-throughput, time-sensitive identifiers. Here, a sequencer is used to advance timestamps, machine identifiers, or counters, ensuring each new ID is unique and sortable.
In money modeling, sequencers are an elegant way to represent currency. For example, a sequencer can loop through the atomic form of a currency, like cents for a dollar, which helps to explicitly model these concepts within a domain. A cents sequencer advances until it reaches its boundary, at which point it wraps and increments the parent dollars sequencer. This approach is easily adaptable to other currency systems with different subunits.
Testability
Testing sequencers is straightforward because they isolate their behavior. This makes them ideal for unit testing, as their state transitions are deterministic and predictable.
describe("Sequencer", () => {
it("wraps correctly when incrementing", () => {
const s = new Sequencer(0, 2);
expect(s.next()).toBe(1);
expect(s.next()).toBe(2);
expect(s.next()).toBe(0); // Wraps after hitting the max
});
it("wraps correctly when decrementing", () => {
const s = new Sequencer(0, 2);
s.current = 0; // Start at the min boundary
expect(s.previous()).toBe(2); // Wraps back to max
});
it("handles a custom step size correctly", () => {
const s = new Sequencer(0, 5);
expect(s.next(3)).toBe(3);
expect(s.next(3)).toBe(0); // Wraps after exceeding max
});
});Because the sequencing logic is encapsulated within the object, its behavior is highly predictable and easy to validate, ensuring the reliability of your system’s progression logic.
For robust assurance, consider property-based testing to verify invariants, for example, that the sequencer’s current value is always between its min and max, regardless of step size or direction.
You can also apply fuzz testing by generating random step sizes, directions, and sequence lengths to ensure consistent boundary behavior under unpredictable usage.
Common Anti-Patterns
While the Sequencer Pattern is a powerful tool, it’s important to use it judiciously. Here are a few more anti-patterns to be aware of:
- Over-engineering simple progressions. Not every bounded counter needs to be a full-fledged Sequencer. If your progression is simple, isolated, and doesn’t need to trigger other progressions, a simple counter with a modulo operator might be sufficient. The added complexity of a sequencer is best reserved for systems that require composability, event hooks, and dynamic behavior. Using the pattern for a basic, one-off loop adds unnecessary overhead and obscures the code’s intent.
- Ignoring event hooks for composition. A key benefit of the Sequencer Pattern is its ability to elegantly handle cascading effects (e.g., a minute ticking over to an hour). A common anti-pattern is to use a sequencer but then manually check its state from an external component to see if a wrap has occurred. Instead of writing code like if (minutes.next() === 0) { hours.next(); }, you should embrace the pattern’s design and rely on the onWrap()event hook. This decouples the sequencers and allows the child sequencer to be fully responsible for notifying its parent, creating a cleaner and more maintainable system.
Contextual Placement
The Sequencer Pattern belongs to the Behavioral Patterns category because it governs how objects change state over time in a controlled, repeatable manner.
Its conceptual roots stretch into electronics, particularly ring counters in digital circuits and modular arithmetic in mathematics, both of which inherently deal with bounded values that wrap at a limit. These inspirations make it naturally adaptable to software domains where cyclical or bounded progression is a core concern.
Conclusion
The Sequencer Pattern offers a formalized solution to a problem many developers face implicitly: managing bounded progressions. Whether you’re cycling through frames in an animation, managing ticks in a simulation, or rolling over financial counters, this pattern provides a reusable abstraction for structured advancement.
By giving a name and shape to the familiar “bounded counter” behavior, the pattern makes progression logic testable, observable, and composable. The result is cleaner, more reliable systems built on clearly defined rules.
Formal Pattern Reference
Table 1: Formal reference for Sequencer Pattern
| Field | Content |
| Pattern Name | Sequencer Pattern |
| Intent | Represent bounded, step-wise progression of values with optional wraparound and composability. |
| Problem | Modeling cyclic or bounded progression is complex and error-prone. |
| Solution | Use a Sequencer to encapsulate this logic. |
| Structure | Sequencer objects that hold state, emit events, and can be composed. |
| Consequences | Pros: Clean, testable logicComposableClear boundary behavior Cons: Requires careful composition when bounds are variable |
| Known Uses | Time libraries, financial ledgers, animation engines, interval scheduling |
Call to Action
The Sequencer Pattern isn’t just a design tool; it’s a mental model for recognizing and taming cyclical structures in any domain.
To see if this pattern can simplify your code, take a closer look at your current projects. In areas like scheduling, animation, UI state, date handling, or currency logic, ask yourself:
- What values advance step-by-step?
- Where do boundaries exist, and what happens when they’re crossed?
- Could a sequencer make that logic cleaner and more robust?
By thinking in terms of bounded progressions, you can identify opportunities to replace scattered, ad-hoc logic with a reusable and predictable control structure.
Leave a Reply